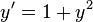Es decir, la segunda derivada de cada función es la propia función con signo inverso. Dentro del espacio funcional de dos dimensiones V, que consiste en todas las soluciones de esta ecuación.
Dado que las funciones seno y coseno son linealmente independientes, juntas pueden formar la base de V. Este método para definir las funciones seno y coseno es esencialmente equivalente a utilizar la fórmula de Euler. Además esta ecuación diferencial puede utilizarse no solo para definir al seno y al coseno, con ella también se pueden probar las identidades trigonométricas de las funciones seno y coseno.
Además, la observación de que el seno y el coseno satisfacen y′′ = −y implica que son funciones eigen del operador de la segunda derivada.
La función tangente es la única solución de la ecuación diferencial no lineal.
satisfaciendo la condición inicial y(0) = 0. Existe una interesante prueba visual de que la función tangente satisface esta ecuación diferencial.